回帰分析の実行

このコンテンツでは、　Spotfireの標準搭載されている「回帰モデリング」の機能を利用して、回帰分析を実行する方法について説明します。 身体測定データの「ソフトボール投げ」の結果を題材に、関連がある変数を利用して、ソフトボールの飛距離を予測します。

なお、本コンテンツで利用したSpotfireのバージョンは10.10/11.4です。ご利用環境によって、一部画面構成が異なりますので、ご了承ください。

身体測定データについて

サンプルファイル

本コンテンツで利用するサンプルファイルは小・中学校の体力測定に関するデータです。こちらからダウンロードしてください。

このファイルをSpotfireに取り込みます。
Spotfireに読込み後、画面左側のノートマーク「分析内のデータ」フライアウトよりデータの内容を確認できます。小学校と中学校の男女に関する、体力測定の結果が含まれています。

回帰分析とは

回帰分析とは、数値を予測する機械学習のタスクの１つです。例えば「各学生の国語の点数から、英語の点数を予測する」といったように、与えられたデータから関係式を仮定し、データに最も当てはまる係数を求めます。
この「国語の点数」のように、説明する側の変数のことを「説明変数」、「英語の点数」のように、説明される側の変数のことを「目的変数」と呼びます。
また、説明変数Xを利用して目的変数Yを予測する関係式を「回帰式」と呼び、この回帰式を作成することを「モデル化」と呼びます。

では、Spotfireを利用して、回帰分析を実行していきます。「ツール」メニューから「回帰モデリング」を選択してください。

　

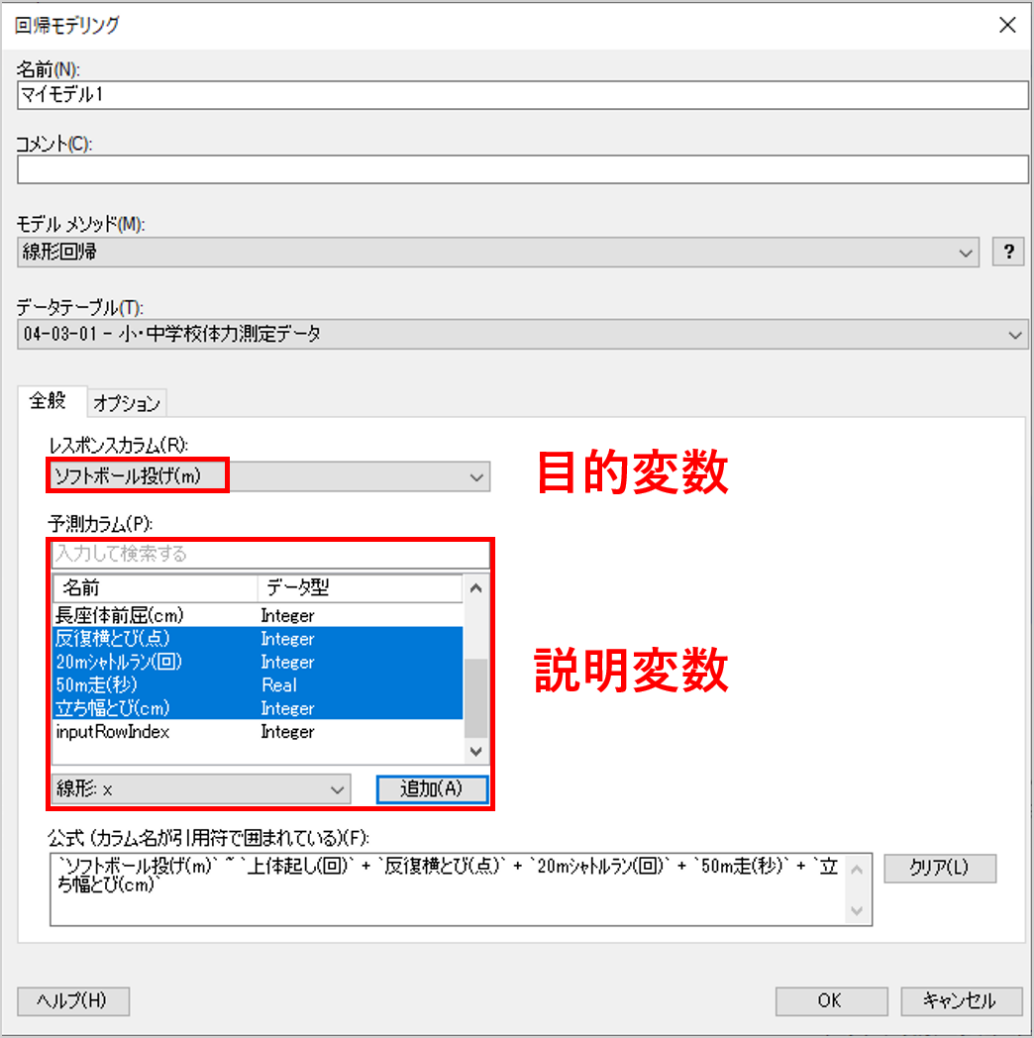
「回帰モデリング」のダイアログが開きます。ここでは、「モデルメソッド」は「線形回帰」、「データテーブル」には取り込んだデータを選択します。
「レスポンスカラム」には、モデル化の対象とする目的変数のカラムを選択します。今回は「ソフトボール投げ(m)」を選択します。
「予測カラム」には、レスポンスカラムを導き出すために使用する説明変数のカラムを選択します。以下の５つの変数を選択して、「追加」ボタンを押してください。

• 20mシャトルラン
• 立ち幅跳び
• 50m走
• 上体起し
• 反復横とび

　

「OK」を押すと、回帰分析が実行され、分析結果の新規ページが生成します。

モデルの要約

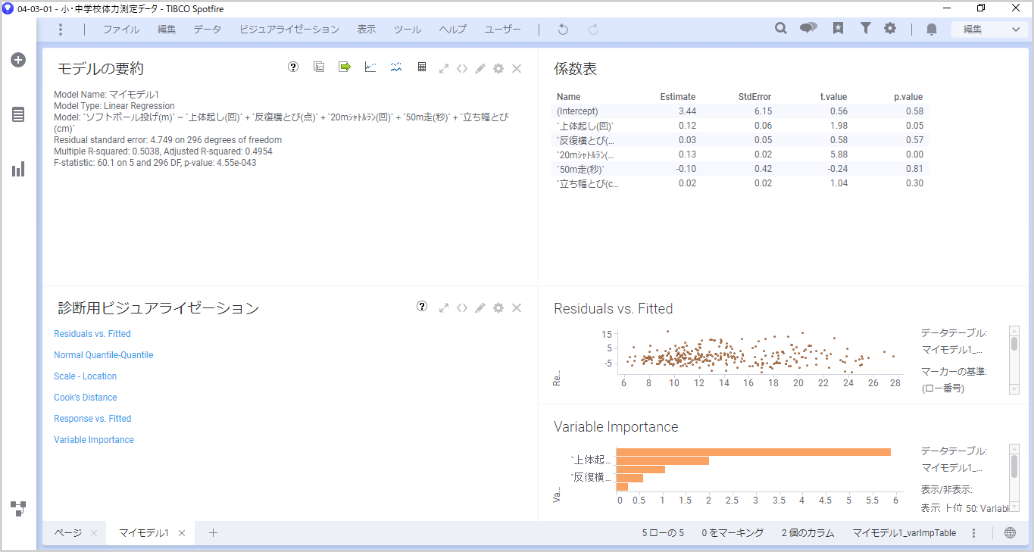
モデルの要約画面を確認します。
Multiple R-squaredは、「決定係数（寄与率）」と呼ばれ、予測モデルの精度を客観的に表す指標の１つです。0から1までの値をとり、1に近ければ精度が高いモデルと解釈されます。

今回の結果では、0.5038となっています。

モデル式自体を採用するかはビジネス判断によるところですが、この0.5前後の値自体は精度が高いと言えるものではなく、改善が必要です。

なお、Adjusted R-squaredは自由度調整済決定係数（寄与率）と呼ばれる指標です。決定係数は、説明変数の数を増やした場合に値が大きくなる傾向にあるため、その影響を調整した指標となります。説明変数の数が異なるモデル同士でその精度を比較する場合には、Adjusted R-squaredを参照するとよいでしょう。

係数表

係数表の画面を確認します。
係数表では、実際の回帰式が読み取れます。NameとEstimateの行を見てください。 Interceptは切片で、それ以外は各説明変数の影響度合いを示す偏回帰係数を表しています。

係数表のEstimateの値をもとに、今回の回帰式を表すと以下の通りです。

モデルのフィッティング

左下の診断用ビジュアライゼーションから「Response vs. Fitted」をクリックしてください。実測値と予測値を散布図で表し、モデルの適合度合いを確認できます。

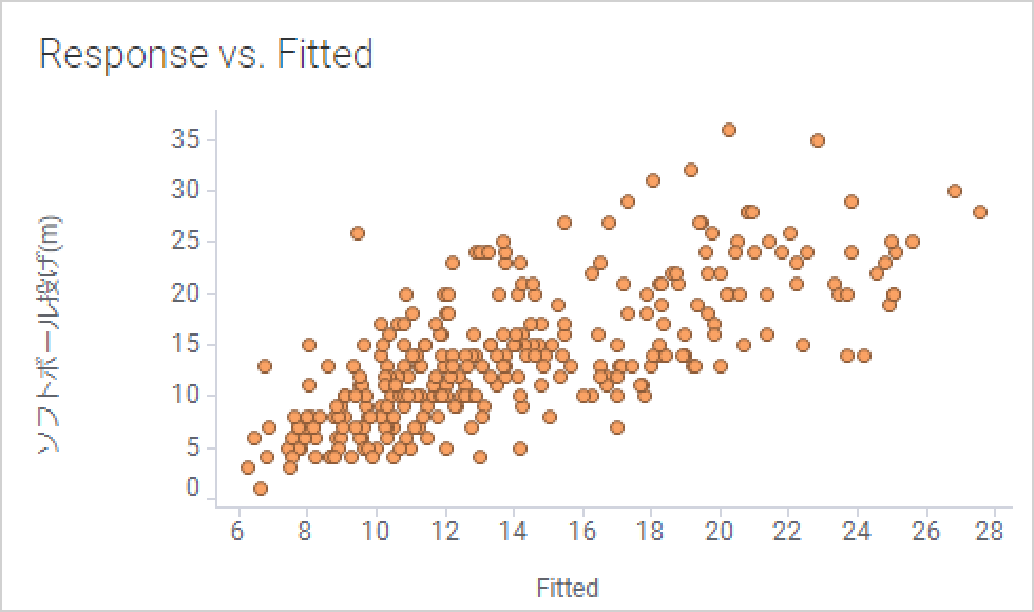
左下の診断用ビジュアライゼーションから「Response vs. Fitted」をクリックしてください。実測値と予測値を散布図で表し、モデルの適合度合いを確認できます。

なお、この散布図に回帰線やラベルを追加する方法は、こちらの記事（パラメータの関連性を把握）を確認してください。

モデルの修正

より精度を高めるために、モデルを修正していきます。
初回のモデリングでは利用していない、学生の属性データを説明変数に追加してみます。 以下のカラムを説明変数として追加します。

• 学校
• 男女

「モデルの要約」画面右上の「モデルの編集」ボタンをクリックすると、「回帰モデリング」ダイアログが再度表示され、作成したモデル設定を変更できます。

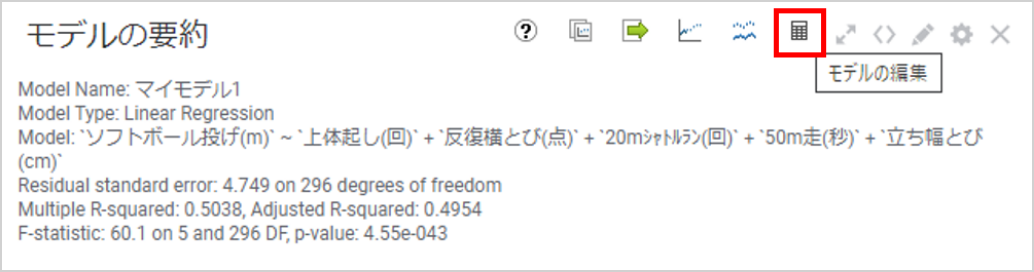
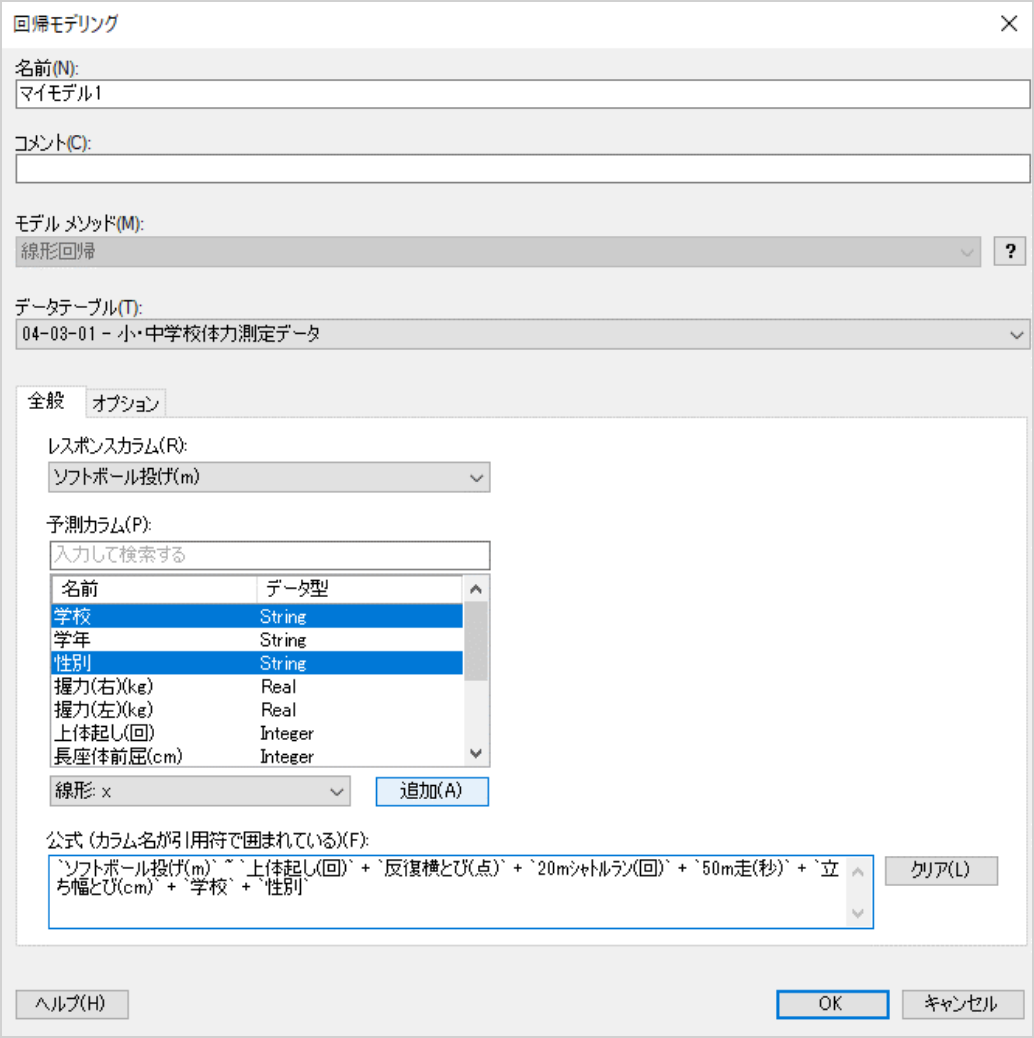
説明変数に「学校」「性別」を追加してください。完了したら「OK」をクリックすると、回帰分析が再実行されます。

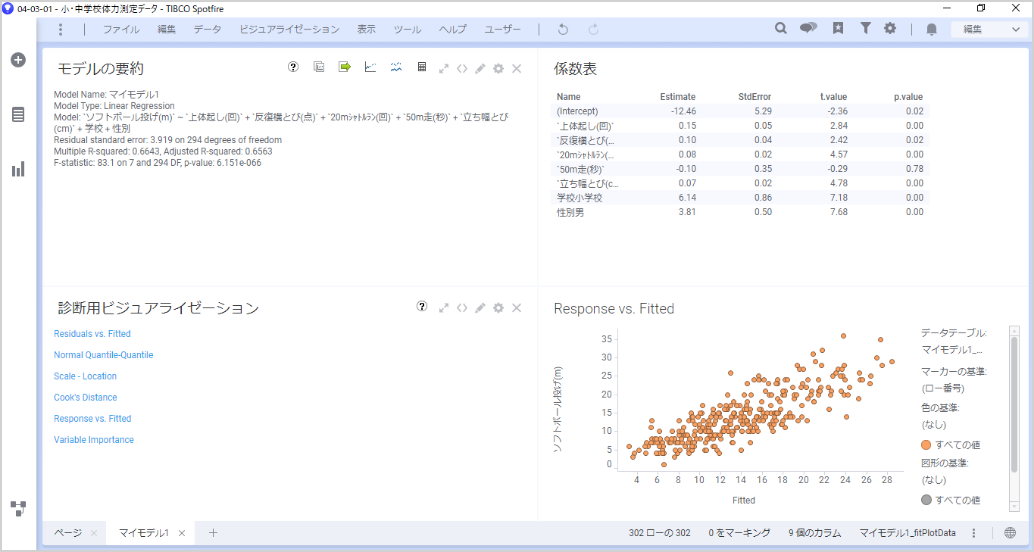
決定係数Multiple R-squaredの値が 0.6643なりました。また自由度調整済み決定係数Adjusted R-squaredの値も高くなり、精度が高まったと言えそうです。モデル修正前よりResponse vs Fittedの散布図もばらつきが少なくなりました。
係数表も更新されており、以下のような回帰式と解釈できます。

「小学生ならば6.14、男性ならば3.81のポイントが追加される」という回帰式です。男子の方が飛距離が伸びるのは理解できる一方で、小学生の方が中学生よりも飛距離が伸びるという結果は解釈が難しい結果となりました。

体力測定データを使ってソフトボールの飛距離を予測できることがわかりました。またモデルを修正することで、より精度が高いモデルを作成できました。今回作成したモデルはファイル内に保存できるため、データを更新した際に予測値を計算できます。

まとめ

今回は、体力測定データを使ってソフトボールの飛距離を予測できることがわかりました。また、モデルを修正することで、より精度が高いモデルを作成できました。今回作成したモデルはファイル内に保存できるため、データを更新した際に予測値を計算できます。

回帰モデリングに代表される、機械学習による予測や分類タスクは、さまざまなビジネスへの応用も可能です。製造業の場合、製造工程における品質データと様々なセンサーデータから、製品の不良品予測ができます。またサービス業の場合、会員の解約予兆を捉えたり、購買予測に利用できます。