相関関係と因果関係の違いを事例から解説

１．相関関係と因果関係の違い

相関関係とは

相関関係とは、ある要素とある要素が互いに関係し合っていることを指します。
以下が相関関係している要素の代表例です。
・子供の「数学の点数」と「理科の点数」
→数学の点数が高い子は理科の点数も高い傾向があり、反対に理科の点数が低い子は数学の点数も低い傾向がある。
・高齢者の「運動量」と「体力」
→運動量が増えると体力も増えるが、体力が減ると運動量も減る傾向がある。
画像①

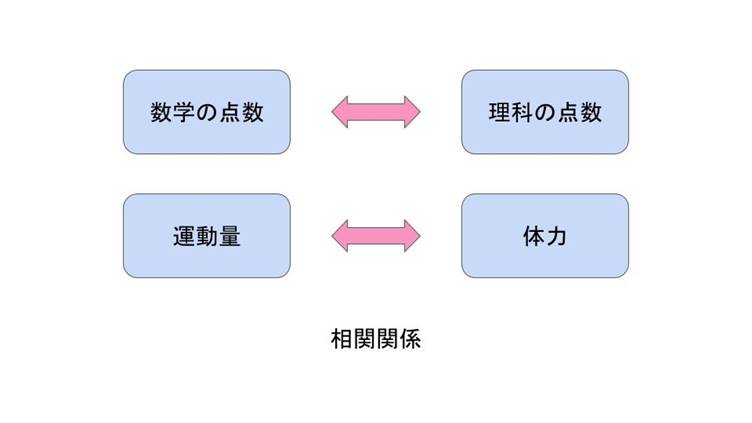
これらはいずれも片方が増えるともう片方も増える相関関係を表しており、このような相関関係を”ある要素とある要素が正の相関関係を示す”と表現します。
また以下のように片方が増えた際にもう片方が減る場合も相関関係があります。
・高齢者の「自宅の滞在時間」と「体力」
→自宅の滞在時間が増えると体力が減り、体力が増えれば自宅の滞在時間が減る傾向がある(外出の機会が増えるため)。
この場合は”ある要素とある要素が負の相関関係を示す”表現します。
ちなみに「数学の点数」と「食事量」のような片方の要素にもう片方の要素が関係しないものは相関関係がないと言います。

因果関係とは

因果関係とは要素同士が原因と結果の関係にあり、ある要素が原因である要素に影響を与えていることを指します。
相関関係との違いは、関係性を示す矢印が双方向ではなく片方向だけであることです。
そのため要素Aと要素Bが因果関係にある場合、要素Aが変化したときに要素Bが変化することはあっても、要素Bが変化したときに要素Aが変化することはありません。
以下が因果関係している要素の代表例です。
・「気温」と「アイスクリームの販売数」
→気温が高くなればアイスクリームの販売数も増えるが、アイスクリームの販売数を増やしたところで気温が高くなることはない。
・子供の「身長」と「足の速さ」
→身長が高い子ほど足が速い傾向があるが、足が速くなれば身長が高くなるわけではない。

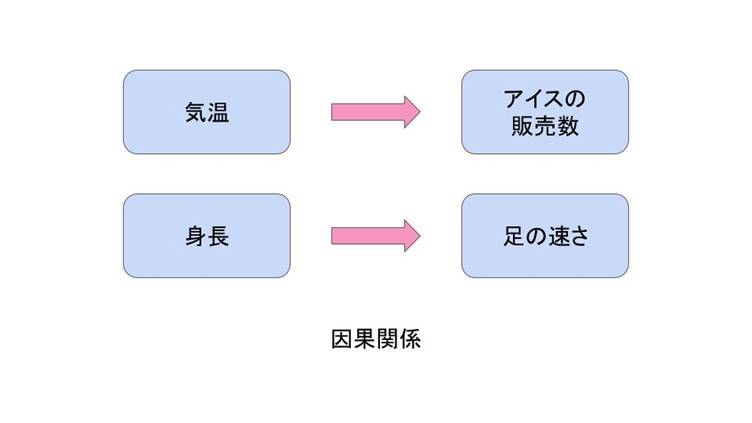
相関関係の例で示した子供の「数学の点数」と「理科の点数」はどちらかの点数が原因でどちらかの点数が変わるわけではありませんので、これらは相関関係ではあっても因果関係ではないと解釈することができます。
このように相関関係と因果関係は同じではなく、因果関係の方がより要素間の関係性に厳しい制約があります。

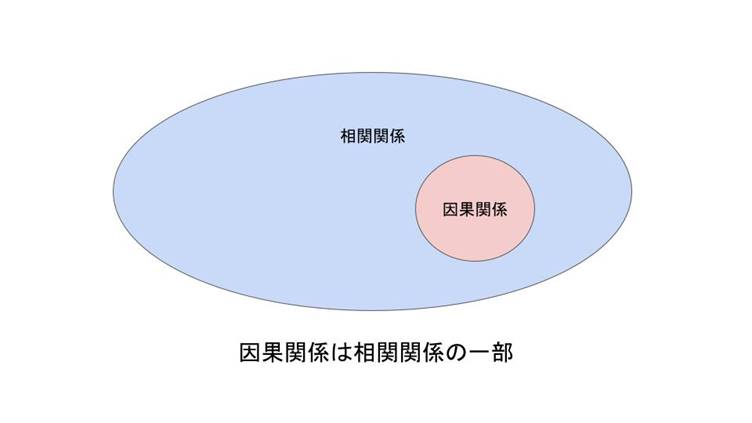
次に相関関係と因果関係を混同してしまった場合、どのようなリスクがあるのかみていきましょう。

２．相関関係と因果関係の違いを混同するリスク

失敗例①〜マーケティングの失敗事例〜

ある保険会社が保険契約率をあげるために過去の顧客データの分析をしました。
最初にどのような顧客が保険を契約してくれる確率が高いか確かめるために各データと契約率の関係性を調べました。
すると顧客一人あたりの訪問回数が多ければ多いほど保険の契約率が高いことが判明しました。
そのため翌年から積極的に顧客一人あたりの訪問回数を増やすよう営業部門に伝達を行いました。
しかしその結果、なんと契約率が下がってしまいました。
なぜこのようなことが起こってしまったのでしょうか。
これは相関関係と因果関係を理解していなかったのが原因です。
詳しく検証をすると、実は保険を契約してくれそうな顧客には積極的に何度も訪問するようにしているとのことでした。
つまり訪問回数が多いから契約率が高いのではなく、契約率が高そうだから訪問回数が多くなっていたということです。
そのためむやみに訪問回数を増やしたところで、逆効果となってしまったというわけです。
データ分析の段階で、相関関係だけでなく因果関係についてもちゃんと検証していればこのようなことにはならなかったでしょう。

失敗例②〜食事管理の分析〜

もう一つ失敗例を紹介しておきましょう。
ある栄養士が肥満傾向の人の間食内容を分析し、食事指導に役立てようと考えました。
肥満傾向の方の間食を分析すると、肥満傾向の方は正常な方と比べてノンカロリー飲料を多く飲む傾向がありました。
そこで栄養士は「実はノンカロリー飲料は、肥満に繋がる飲料である」と解釈しました。
早速食事指導の際にノンカロリー飲料を飲まないよう指導しました。
しかしその行動は肥満改善に全く効果がありませんでした。
それどころか逆に肥満を増強させる結果になってしまい、患者様からの信頼を失ってしまうことになりました。
なぜこのようなことが起こってしまったのでしょうか。
実は、肥満の方はこれ以上太らないようにノンカロリー飲料を飲むようにしていただけで、ノンカロリー飲料の摂取量が肥満に繋がっていたわけではなかったからです。
ノンカロリー飲料が原因で肥満になったわけではなく、肥満が原因でノンカロリー飲料の摂取量が増加していたというわけです。
この場合肥満とノンカロリー飲料の間に因果関係はありますが、意図していた方向とは反対向きの因果関係でした。
このように因果関係を考える時は、相関関係との違いだけでなく因果関係の向きにも注意が必要です。
今回は少々おおげさな例でしたが、当事者だと案外このような簡単なミスをしてしまうことはあります。

３．相関関係と因果関係の判別方法

ここまでで様々な例を使って相関関係と因果関係の違いを理解していただきました。
では実際にデータ分析をする時に相関関係なのか、因果関係なのか、どのように判別すればよいかご説明していきましょう。

相関関係の判定方法

相関関係はデータ分析で簡単に判定することができます。
データ間の関係性だけ分かればよいので、相関分析という手法を使うことで判別できます。
相関分析ではp値というものが算出されますが、一般的にp値が0.05(5%)を下回っていれば有意に相関関係があることを示すことができます。
またp値と合わせてr値(相関係数)を算出することで、
「正の相関関係、負の相関関係のどちらなのか」
「どれくらいの強さの相関関係なのか」
も知ることができます。
ちなみに相関係数が-1から1の間の値をとり、1に近づけば近づくほど強い正の相関があり、-1に近づけば近づくほど強い負の相関があると解釈します。
相関がない場合は、相関係数が0となります。

因果関係の判定方法

相関関係と違い、因果関係の判定をデータ分析の結果のみで行うことは困難です。
なぜならデータ分析から分かるのは要素間の双方向の関係性(相関関係)だけだからです。
しかし本当に知りたいのは相関関係ではなく、因果関係である場合は多くあります。
手持ちのデータから因果関係まで推測しなければいけない場合に、因果関係を判定する方法を説明していきましょう。
基本的には相関関係が示された要素を見比べ、理論的に考察をして因果関係を判定していきます。
要素間の因果関係に理論が成り立つのであれば、因果関係があると判定する場合が多いです。(厳密な因果関係の証明方法は後ほど紹介します)
例えば気温とアイスクリームの販売数の相関関係が示されたのであれば、気温が原因でアイスクリームの販売に影響を与えることは理屈上、十分考えられる内容であるため、因果関係を表していると判断してしまってよいと言えます。
このように確実な方法ではありませんが、考察をすることで因果関係を推定できるケースはよくあります。
しかし先ほどの失敗例①のように、訪問回数と契約率の間に因果関係があるかどうかは考察だけで断定しきれません。
一番簡単な解決方法としては、実際の営業担当者にヒアリングなどを行い推測した因果関係が妥当であるかどうか確認するのが良いでしょう。
それが難しい場合、またはそれでも分からない場合は、少し大変ですが特殊なテストで因果関係を証明していく必要があります。

４．因果関係を証明したい時はどうすればよいか

RCT(ランダム化比較試験)

データ分析だけで因果関係を証明したい場合、基本的にはRCT(ランダム化比較試験)と呼ばれるテストが必要になります。
RCTはマーケティングの分野でABテストと呼ばれることもあります。
ランダム化比較試験とは特別な介入をする人としない人をランダムに選定し、介入群と非介入群で最終効果を比較する方法です。
先ほどの失敗例①ですと、一部の地区で訪問回数を増やす顧客と今まで通りの対応をする顧客をランダムに2群に分け、最終的な契約率を2群間で比較することで訪問回数と契約率の因果関係を証明することができます。
このようなテストを事前に行っておくと、因果関係の失敗をするリスクを下げることができます。
RCTを行うのは確かに手間がかかりますが、リスクの高い施策を決定する際はRCTで事前に因果関係を検証しておくことが不可欠です。

傾向スコア分析

因果関係を示す最適な方法は先ほど紹介したRCTですが、時間的な問題や倫理的な問題でRCTが実行できない場合があります。
この場合は傾向スコア分析と呼ばれるものを使って因果関係を証明することが出来る場合があります。
傾向スコア分析について簡単に説明していきましょう。
先ほどの失敗例①では、訪問回数が多い人たちと少ない人達で契約してくれそうな確率がそもそも異なっていたことが問題でした。
そのため、初期接触の時の感触(今後契約してくれそうかどうか)が同じだった人たちだけで比較してその問題を解消してしまおうという考え方が、傾向スコア分析の基本的な考え方です。
まずは今後の訪問回数に影響するデータをなるべく網羅的に収集します。
この時にデータの抜けがあると傾向スコア分析が上手く行えませんので、注意が必要です。
次に、そのデータを使ってロジスティック回帰分析などで訪問回数が多くなりそうか、少なくなりそうか一人ずつ予測します。
最後にその予測値が同じまたは近い者同士でペアにして、実際の訪問回数と契約率の間に相関があるか比較します。
事前に今後の訪問回数に影響する要素を統一した上で比較を行うことになるので、ここで相関が認められれば因果関係があると判定できることになります。
ただし傾向スコア分析は必要なデータが全て揃っていることが前提の解析であり、そこに少しでも誤りがあると間違った結果を出してしまうリスクがあります。
ランダム化比較試験が行える場合は、なるべくそちらの方法で因果関係を確かめるようにしましょう。

５．相関関係と因果関係の違いを気にしなくても良い場合

ここまで相関関係と因果関係を混同するリスクについてお話してきましたが、因果関係を気にしなくても良い場合があります。
それは、データ分析の目的が検証ではなく予測だけである場合です。
データから何かを予測する場合、予測するものとデータの間が相関関係でも因果関係でも予測精度に大きな差は生じません。
ここでも簡単な例を使って説明していきましょう。
鶏が鳴くことと、日が昇ることは過去のデータから相関関係にはあることが分かっています。
しかし鶏が鳴くことが原因で日が昇るわけではありませんので、因果関係はないと言えます。
日が昇る原因を特定することが目的であれば、もちろん因果関係を考えながら分析をしなければなりません。
しかし日が昇る時間を予測するだけであれば、相関関係だけでも十分です。
なぜなら因果関係はなくても鶏が鳴いたタイミングで日が昇る傾向があるという事実は変わらないからです。
そのため鶏の鳴いたタイミングを利用して、精度の高い予測を行うことも可能です。
このように分析の目的が予測だけの場合は、相関関係と因果関係の違いをそれほど気にする必要はありません。

６．まとめ

最後に相関関係と因果関係についておさらいをします。

データ分析の現場では、相関関係と因果関係を混同してしまっているケースがしばしば見受けられます。
しかしこれらの違いを知らずにデータ分析の結果を解釈するのは非常に危険です。
間違った解釈をしないためにも、相関関係と因果関係の違いをしっかり理解しておきましょう。
最後までお読み頂きありがとうございました。