共分散構造分析(SEM)の活用法や注意点を解説

１．共分散構造分析(SEM)とは

「多くの要素がどのように影響し合っているのか」「収集したアンケート結果から、各質問間の関係性を簡潔にまとめたい」などリサーチ分析を行っていると疑問や課題が生まれます。

共分散構造分析（SEM：Structural Equation Modeling）は共分散と呼ばれる数値を利用して、互いに関連を持つ複数の要素間の関係性やその程度をモデル化する分析です。
共分散構造分析によって今まで複雑でよく分からなかったデータ同士の関係性が、ひと目で理解することができるようになります。

イメージをつけるために、まずは簡単な例を紹介します。
学生の総合学力を決める要因を探ることが今回の分析の目的です。
データは今までに生徒たちが受けてきたテストの点数があります。
その場合、以下のようなモデルを使って学力を表すことができます。

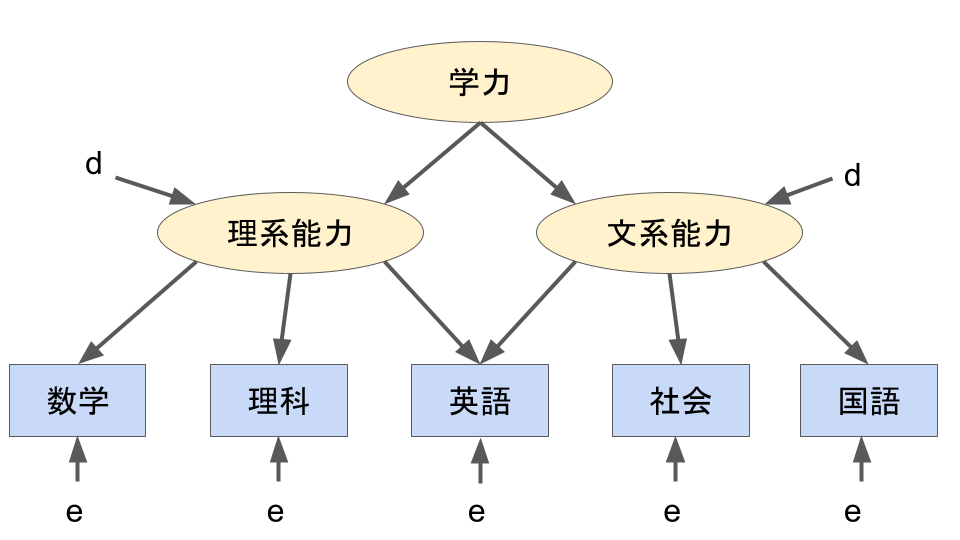
このモデルは「学力は理系能力や文系能力に影響するだろう」「理系能力は数学や理科、英語の点数に影響するだろう」「文系能力は国語と社会、英語の点数に影響するだろう」という仮説に基づいて作られたものです。

このようにモデル化するだけでもイメージがしやすくなりますが、この図だけでは
”どの要素がどのくらい影響しているのか”
”この仮説が本当に妥当なのか”
を知ることはできません。

そこで共分散構造分析の出番です。
共分散構造分析を使ってどれくらい影響しているのか算出してみると、このようなモデルが完成します。

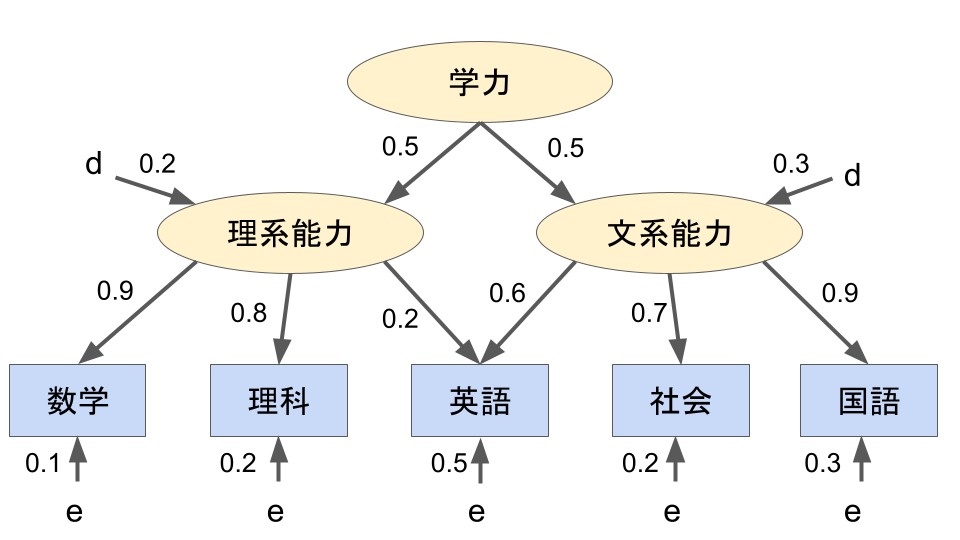
こうして影響の強さを数値にして表すと、より要素間の関係性を知ることができるようになります。
ちなみにeやdという文字は誤差（観測しきれていない要素）を示します。
今回の結果だけから考察すると、英語の点数を上げるためには理系よりも文系能力のアップが重要になることが分かります。（これはあくまでサンプルですので、実際の結果とは異なります）
このように共分散構造分析を使えば要素間の複雑な関係性を分かりやすくモデル化することができます。

では実際に共分散構造分析がどのように活用されているか、例をみてみましょう。

２．共分散構造分析の活用例

例①〜マーケティング企画立案〜

ある商品の売上を改善するための施策を考えたいのですが、どこから改善していくべきか検討がつかない状況です。
そこで共分散構造分析を使うことで、売上に影響する要素の関係性を分かりやすくモデル化してみることにしました。

まずは売上がどのような要素で成り立つのか、仮説を立てながらモデルを作ります。
最初に売上を構成するのは”Preference(好意度)”、”Awareness(認知)”、”Distribution(配荷)”の3要素だと仮説を立てました。

次にそれら3要素を構成する要素の候補をデータ化できるもので設定していきます。
また”Awareness(認知)”と”Preference(好意度)”は”Distribution(配荷)”とも関係し合うことが想定されたため、それもモデルに加えました。

以上の仮説を踏まえて作られたモデルが以下の図です。

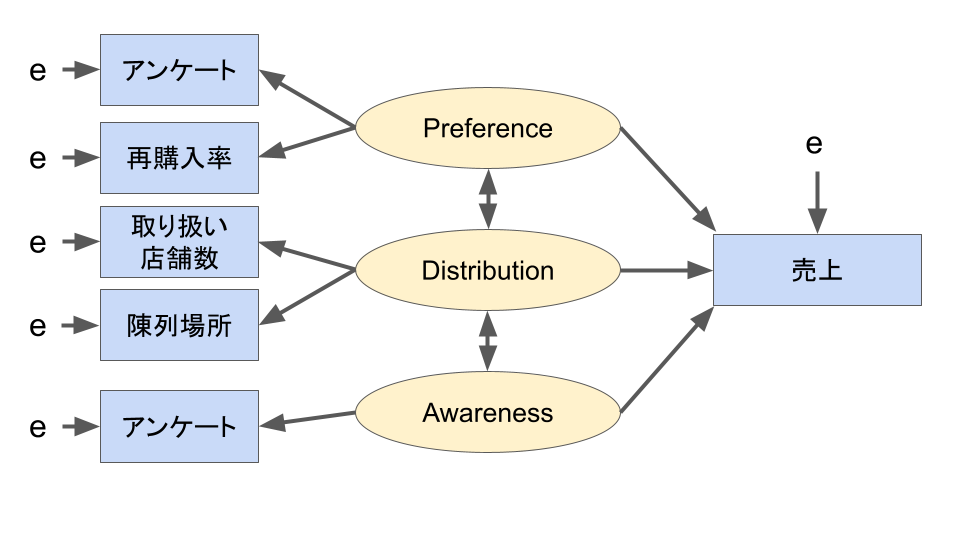
売上を構成する要素が分かりやすくなりました。
直接測定できない要素(潜在変数)は丸で、測定してデータ化できる要素(観測変数)は四角で表現しています。

ここからいろいろな地域や同じカテゴリーの商品のデータを使って、どの矢印がどのくらい影響力を持っているのか共分散構造分析によって算出していきます。

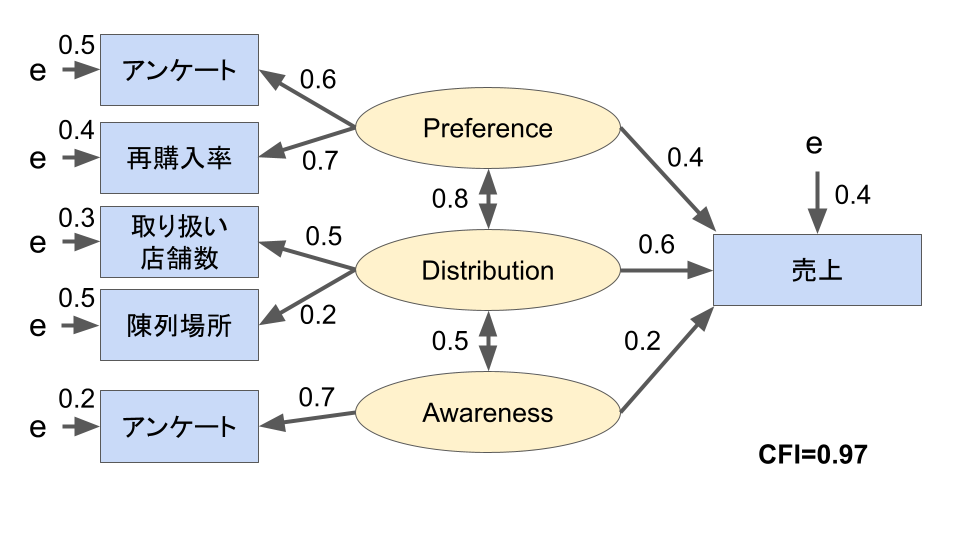
ちなみにCFIの値はこのモデルの適合度(妥当性)を表す指標の一つで、0から1までの範囲に収まります。
1に近いほど適合が良く、一般には0.95以上であればよいモデルと判断します。
今回のCFI=0.97という値はこのモデルが非常に適合していることを示します。

この結果からこの商品の売上に影響力を持つのは”Distribution(配荷)”であることが想定され、優先的に強化を検討する必要があることが分かりました。

例②〜アンケート結果の分析〜

共分散構造分析がよく使われるデータの一つが、アンケート結果のデータです。

ある企業が社員のストレス状態を分析するためにストレスチェックアンケートを実施しました。
そのアンケートから各要素の関係性を分析し、社員のメンタルケアを目指したいと思っています。

アンケートの各設問は”身体的ストレス”、”精神的ストレス”、”労働時間による負担”、”人間関係の負担”のいずれかを表すもので構成しました。
共分散構造分析を行うために、以下の仮説を立てました。
・”身体的ストレス”と”精神的ストレス”は互いに相関する
・”労働時間による負担”は”身体的ストレス”、”精神的ストレス”のどちらにも影響を及ぼす
・”人間関係の負担”は”精神的ストレス”に影響を及ぼす

これらの仮説を元に以下のモデルを作成し、共分散構造分析を行いました。

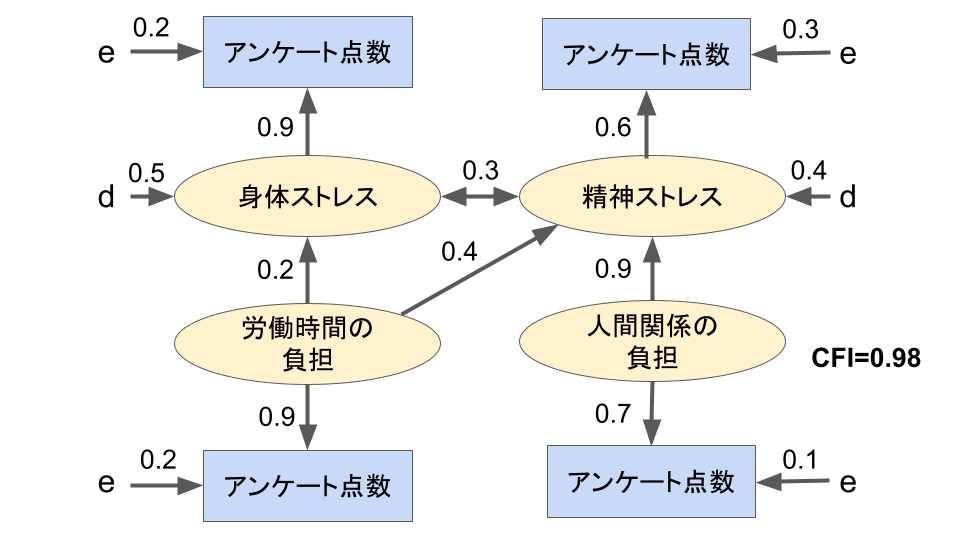
CFIは0.98であり、モデルがよく適合していることが分かりました。

この結果から最初に立てた仮説は概ね妥当であることが示されましたが、さらに”労働時間による負担”は”身体的ストレス”よりも”精神的ストレス”に大きく影響を及ぼすことが分かります。
また”人間関係の負担”が他の要素と比べて”精神的ストレス”に大きな影響を与えていることが分かりました。

以上の結果から、社員の人間関係改善に向けた取り組みが必要であることが分かりました。

３．共分散構造分析を使うメリット

複雑な複数の要素に対応できる

共分散構造分析はたくさんの要素間の関係性を一度に計算することができます。
これは相関分析や重回帰分析などではできないことで、共分散構造分析の最大のメリットです。

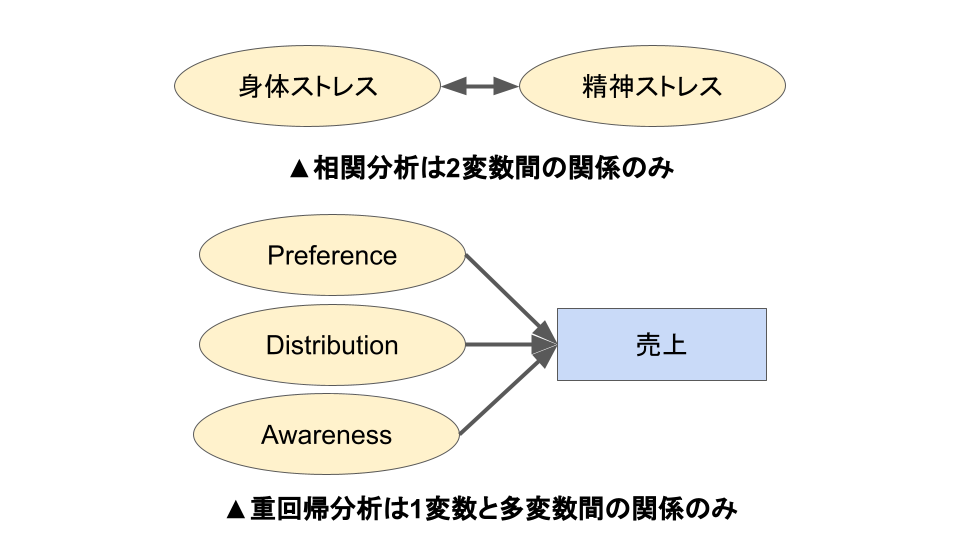
実際のデータは複雑に各要素が影響し合っている場合がほとんどです。
ですので、複雑なモデルに対応できる共分散構造分析はより現実を反映した結果を出してくれます。

結果が分かりやすい

共分散構造分析は仮説をベースにモデルを作るため、結果を一枚の図に表すことができます。
そのため統計やデータ解析の知識がない方でもひと目で結果を解釈することができます。
結果の図はそのままプレゼンテーションなどに活用できるため、非常に便利です。

４．共分散構造分析を行うときの注意点

ここまで共分散構造分析の優れた点を紹介してきましたが、注意しなければ行けない点もあります。
実際に解析するときは以下の点に注意してください。

モデルの作成が難しい

共分散構造分析を行う際は最初に仮説を立て、構造モデルを作る必要があります。
慣れないうちはこのモデル作りが大変です。
というのも、最初の段階でおかしなモデルを作ってしまうと妥当な結果が得られないからです。
正確には計算自体はできるのですが、モデル性能が悪いためCFIが低い役に立たないモデルになってしまいます。
分析の過程で多少のモデル修正はできるのですが、あまりにおかしなモデルだと修正も困難です。

このような事態を防ぐために、共分散構造分析を行う前に入念な仮説の設定が必要です。
もし自社内または論文等で、共分散構造分析を似たような事例で適用したものがあれば、それを参考にするのも有効です。
後で泣かないためにも、適当なモデルを作って進めないように注意しましょう。
最初の仮説がいかに妥当かどうかで良い分析の可否が変わってきます。

各要素を表すデータが必要

仮説を立ててモデルを作ったものの、想定した要素を表すデータがとれないと共分散構造分析を行うことができません。
先程の活用例でいえば、「”Distribution(配荷)”を構成する要素の一つに”各店舗での商品の陳列場所”を仮定したものの、その情報を上手くデータにできない」といった状況です。
共分散構造分析はデータよりも仮説を前提とするため、このような状況にはよく陥ります。

対策としては、陳列場所に順位をつける(見出し部であれば1,通常の位置であれば2,一番下または一番上の見にくい位置であれば3)などが挙げられます。
もちろんそもそも陳列場所を示すデータがなければ、どうしようもないので注意が必要です。
データがない場合は、モデルから陳列場所の情報を抜くしかありません。
もちろんその分モデルの精度は落ちますが、データがなければ仕方がありません。
このように仮定した要素をうまくデータの形にする場合は、
”そのデータが上手くその要素を表しているか？”
”そのデータは収集可能か？”
といった点を考慮しなければなりません。

望ましい結果が出ないこともある

どの分析にも言えることですが、正しく分析をしたところで必ずしも望ましい結果になるとは限りません。
望ましくない結果が出たときは、最初の仮説やデータの妥当性に問題がないかもう一度検証してみる必要がありますが、そこに問題がなければそれが現実だと受け入れるようにしましょう。

５．共分散構造分析のアルゴリズム

共分散とは

便利な共分散分析ですが、どのように各数値を算出しているのか説明していきましょう。
まずは”共分散”について説明していきます。
簡単に言うと、共分散とは”ある要素とある要素の相関の程度を表すもの”です。
計算式は「”変数1の偏差”と”変数2の偏差”を掛け算した値の平均値」です。
最初の例を使って”数学の点数”と”理科の点数”の共分散を算出してみましょう。
偏差とは値から平均値を引いたものです。
つまり生徒Aの”数学の偏差”は生徒Aの数学の点数から全体の数学の平均点を引いたものになります。
この方法でまずは生徒ごとに”数学の偏差”と”理科の偏差”を算出して掛け合わせていきます。
最後に生徒数で割って平均値を出せば、それが共分散です。

このように共分散は、簡単な四則演算のみで算出することができます。
数学も理科の偏差も「+」または「-」の生徒数が多ければ多いほど共分散は大きくなっていきます。
したがって、共分散が大きければ大きいほど”数学の点数”と”理科の点数”の相関が強いという判断ができるというわけです。
ちなみに共分散を各変数の偏差で割った値が”相関係数”です。

共分散構造とは

共分散は要素間の相関の程度を表す指標でした。
次に共分散構造について説明していきます。
共分散構造とは、共分散を方程式モデルの母数で表現したものです。
方程式モデルの母数という聞き慣れない単語が登場しました。
これも先ほどの例を使って説明していきましょう。
最初のモデルでは、”理系能力”は数学と理科、英語の点数にそれぞれ影響を与えていました。
数学への影響力をα11、理科への影響力をα21、英語への影響力をα31とすると、各教科の点数は以下の方程式で表すことができます。
数学の点数=α11×理系能力+誤差(e1)
理科の点数=α21×理系能力+誤差(e2)
英語の点数=α31×理系能力+誤差(e3)
誤差をつけるのは生徒によって個人差があるからです。
この3つの方程式のことを方程式モデルと言い、方程式モデルで使われたαや誤差のことを”方程式モデルの母数”といいます。
つまり共分散をこれらの値で表現したものを共分散構造といいます。
実際には各共分散を共分散行列というもので表して、以下のように表現します。

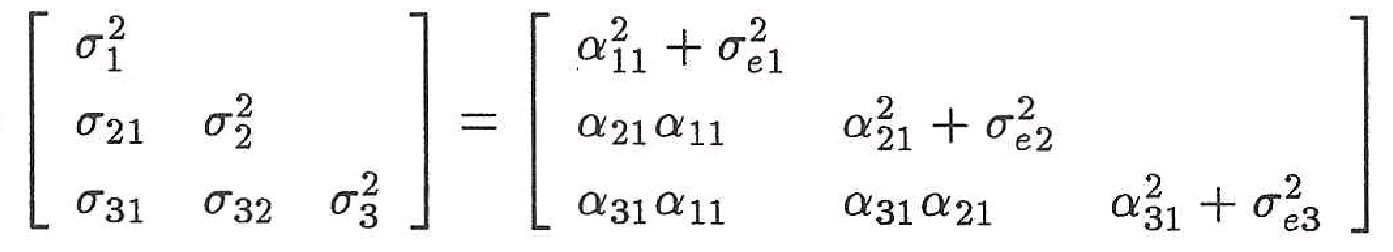
共分散構造分析は、この共分散構造に実際の数値を当てはめて計算することで、α11とα21,α31を算出していきます。(この計算には最尤法や最小二乗法など様々な方法が存在します)
難しい言葉がいくつか出てきましたが、要するに要素同士の相関を方程式に当てはめて各影響力を算出するのが共分散構造分析の概要です。
もちろんモデルが複雑になればなるほど方程式の数が増え、計算も複雑になります。
しかし算出される値は共分散から算出されている点は変わりありません。
その点だけでも覚えておきましょう。

６．まとめ

最後におさらいをします。

共分散構造分析はうまく使えば非常に強力な分析方法です。
しかしその反面、最初の仮説設定や妥当なデータの収集が大変でもあります。
最初は難しいと感じることも多いと思いますが、慣れれば簡単にできるため、是非ご活用を検討してみてください。

最後までお読み頂きありがとうございました。