多次元尺度構成法の活用法を具体的な事例を参考にわかりやすく解説
1.多次元尺度構成法とは
多次元尺度構成法の概要
多次元尺度構成法とは、類似度を元に対象の関係を視覚的に分かりやすい形に変換する分析手法です。
英語でMDS(Multi-dimensional scaling)と表現されることもあります。
分析された結果はポジショニングマップなどのグラフとして活用します。
多次元尺度構成法は複数の変数に対応する多変量解析の一種であり、大量のデータから対象間の関係性を把握する目的で主に使われます。
作成したポジショニングマップは現状把握や今後の方針決定に利用しやすいため、マーケティングの分野と相性の良い分析です。
多次元尺度構成法の活用場面
多次元尺度構成法を活用するのは、”複雑なデータ間の関係性を分かりやすくグラフ化したい時”がほとんどです。
具体的には以下の場面で多次元尺度構成法が活用されます。
- 競合となる他社製品のポジションや関係性をポジショニングマップで把握し、自社製品の開発方針を検討する
- 顧客行動の各地域別の特性をポジショニングマップで把握し、類似性の高い地域でグルーピングして施策を検討する
- 自社の製品をポジショニングマップで比較し、売れる商品と売れない商品の差を検討する
このように多次元尺度構成法は何かの関係性や類似性を把握したいときに活用されます。
結果が数値ではなくポジショニングマップのようなグラフで視覚的に表せるため、プレゼンテーションの場面でも有効活用できます。
多次元尺度構成法を実施する手順
多次元尺度構成法を実施するためには、比較する対象ごとの類似性を示すデータが必要になります。
多次元尺度構成法を実施することが決まれば、まずは類似性を示すデータを作成しましょう。
以下が多次元尺度構成法を実施する際に使う分析用データの例です。
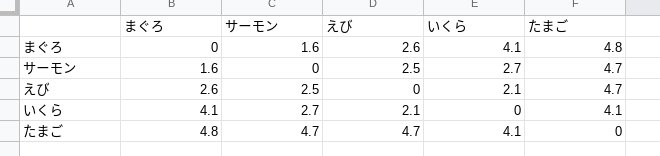
あるお寿司屋さんが5つの寿司ネタのポジショニングマップを作成したいとしましょう。
このデータの数値は各対象間の類似性を5段階で示しており、数値が小さければ小さいほど類似性が高い(性質が近い)ことを示しています。
例えば”まぐろ”と”サーモン”の数値は1.6となっており、類似性が高いことが分かります。
このようなデータは様々な方法で収集・作成できますが、一番多いのはアンケートを使った収集方法です。
アンケートの場合、各対象間に関して”どれくらい似ていると感じるか”を5段階(何段階でも可能)などで評価してもらい、その値を集計したものを分析データとして活用する方法などが挙げられます。
質問例:「”まぐろ”と”えび”はどのくらい似ていると感じるか、5段階でお答えください」
全ての回答の平均値などを使って先ほどの分析用データを作成していきます。
※データ入力時は「とても似ている=1、似ている=2、どちらでもない=3、似ていない=4、全く似ていない=5」とした。
このようなアンケートは検討する対象の数が多ければ多いほど質問数が増えていくため、注意が必要です。(この例では5種類の寿司ネタを比較したため、10パターンの質問が必要でした)
分析用のデータの用意は完了です。
いよいよ多次元尺度構成法を実施できます。
実施後は以下のようなポジショニングマップが生成されます。
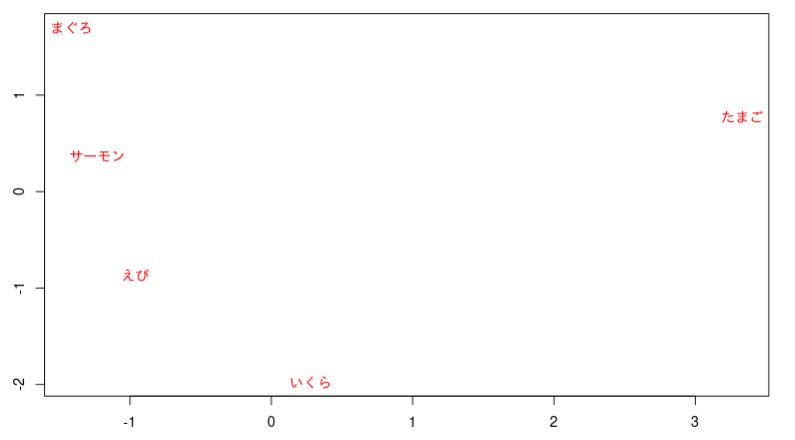
“まぐろ”や”サーモン”、”えび”が比較的近い位置にあるのに対して、”たまご”は他のネタと随分離れていることが分かりますね。
“いくら”も”たまご”ほどではないですが、少し離れた位置にあるようです。
このことから、”まぐろ”や”サーモン”、”えび”は消費者から似ているネタだと認識されていることや”たまご”は他のネタと似ていないと認識されていることが考察できます。
なおx軸とy軸に数字が記載されていますが、多次元尺度構成法の軸の数値は意味を持ちませんので、無視しても構いません。
ポジショニングマップでは対象間の位置関係だけに注目するようにしましょう。
以上が多次元尺度構成法を実施する際のおおまかな手順です。
事前の準備として、分析用のデータを忘れずに用意するようにしましょう。
またアンケート以外のデータの収集方法として、値段やスペックなどの情報を示すデータからユークリッド距離などを用いて分析用データを作成する方法もあります。
2.多次元尺度構成法の特徴
多次元尺度構成法のメリット
複雑な情報を分かりやすく視覚化できる
多次元尺度構成法を使えば、どんなに複雑なデータでも分かりやすいグラフに変換することができます。
100列以上のデータでも問題ありません。
このようなデータでもユークリッド距離などを用いれば対象間の類似性を表すデータに変換することができるため、多次元尺度構成法を活用することができます。
そのため全体から対象間の関係性を俯瞰して検討したい際に、多次元尺度構成法が役立ちます。
ポジショニングマップが簡単に作れる
多次元尺度構成法を活用すれば、ポジショニングマップを簡単に作ることができます。
ポジショニングマップはマーケティングの分野で活用されるグラフです。
他社製品と自社製品間の関係性を検証する際や、既存の製品から差別化した製品を開発する際の指標としてしばしば活用されています。
まずはポジショニングマップで全体を俯瞰し方向性を決めてから、詳細に分析していくという流れが一般的です。
そのような状況でポジショニングマップを作成する際に、多次元尺度構成法が役立ちます。
多次元尺度構成法の注意点
データの準備にひと手間かかる
多次元尺度構成法を行うためには分析用データを作成する必要があるため、注意が必要です。
各対象間の類似性を示すデータの形は一般的ではないため、慣れていないと混乱しやすいためです。
多次元尺度構成法に使う分析データは距離行列と呼ばれます。

先ほどの例で示したようにアンケートから距離行列を作るのはそこまで難しくありません。
反対に100列以上のデータから距離行列を作るためには、特殊な変換が必要なため注意が必要です。
一般的には、この変換にはユークリッド距離と呼ばれるものを使用します。
ユークリッド距離とはピタゴラスの定理を用いて対象と対象の距離を計算することで、その対象間の類似性を表したものです。
このように多次元尺度構成法を活用するためには、分析用データの準備にひと手間かかるため注意してください。
関係性の細かい検証は困難
多次元尺度構成法は対象間の関係性(類似性)を分かりやすく視覚化することが目的であるため、詳しく検証することはできません。
先ほどの例で「たまごが他のネタと類似性が低いと認識されている理由が知りたい」という場合は、別の分析手法を使う必要があります。
多次元尺度構成法は複雑な関係性を分かりやすく表現する分析手法であり、細かく調べる分析手法ではありません。
その点を踏まえた上で上手に活用するようにしましょう。
比較する対象の数を適切にする必要がある
アンケート調査で分析用データを作成する場合、比較する対象の数が増えすぎないように注意する必要があります。
先ほどの例では対象が5つだったため、10パターンの質問で対応できました。
しかしもし対象が10だった場合、45パターンも質問しなければならず、回答者に負担をかけることになってしまいます。
反対に少なすぎるとわざわざポジショニングマップにする必要がなくなってしまいます。
アンケート調査をベースに多次元尺度構成法を行う際は、検討する対象を適切な数にするよう配慮しましょう。
対象の数が多くなってしまう場合は、ユークリッド距離を使って距離行列を作成する方法をとるようにしましょう。
主成分分析やクラスター分析との違い
主成分分析との違い
主成分分析は大量のデータを要約して変数を減らすことができる分析です。
作成した変数の中で、重要度が高い2つの主成分を用いることでポジショニングマップを作成することも可能です。
作成されたポジショニングマップは多次元尺度構成法で作成されたものと似ており、基本的にはどちらの分析手法を使っても問題はありません。
両者の最大の違いは、以下のように”分析を行う目的が違う”ところです。
- 多次元尺度構成法→対象間の関係性をポジショニングマップで示したい
- 主成分分析→データを要約してより少ない変数で表現したい
どちらを使うべきか悩んだ場合は、分析する目的から考えるようにしましょう。
クラスター分析との違い
クラスター分析は対象間の類似性を考慮して、似ている対象同士をグルーピングする分析手法です。
先ほどの例を使ってクラスター分析を行って3グループに分類した場合、以下のような結果が得られます。
グループA:まぐろ、サーモン、えび
グループB:いくら
グループC:たまご
クラスター分析を使えば何と何が似ているのか明確であり、すでにグループ分けもされているため、多くのメリットがあります。
しかしクラスター分析でポジショニングマップを作成することはできません。
以上の理由から、それぞれの分析は目的によって以下のように使い分けられます。
- 多次元尺度構成法→ポジショニングマップを作成したい
- クラスター分析→似ている対象同士でグループ分けしたい
どちらを使うべきか悩んだ場合は、最終的にどのような結果を得たいのかを逆算して分析手法を選択するようにしましょう。
3.多次元尺度構成法の活用事例
多次元尺度構成法を活用して新しい製品開発のポジショニング検討を行った事例
寝具を製作、販売する企業が、新しいまくらを開発することになりました。
まくらの市場での人気は、高さ(厚み)や反発の強さ、通気性、値段など多くの要素によって決まることが分かっています。
しかし要素が多すぎるため、具体的にどこに力を入れてまくらの開発を行うべきか、まだ決まっていません。
そこでまずはすでに売れている他社のまくらを対象にポジショニングマップを作成することで、ポジショニング戦略を検討することになりました。
現在人気がある5種類の他社のまくらを対象にデータを集め、多次元尺度構成法を使ってポジショニングマップを作成することにしました。
このケースでは反発の強さや値段など、そのまくらの性能や特徴を表すデータを集め、ユークリッド距離を用いて距離行列に変換したものを分析用データとして扱いました。
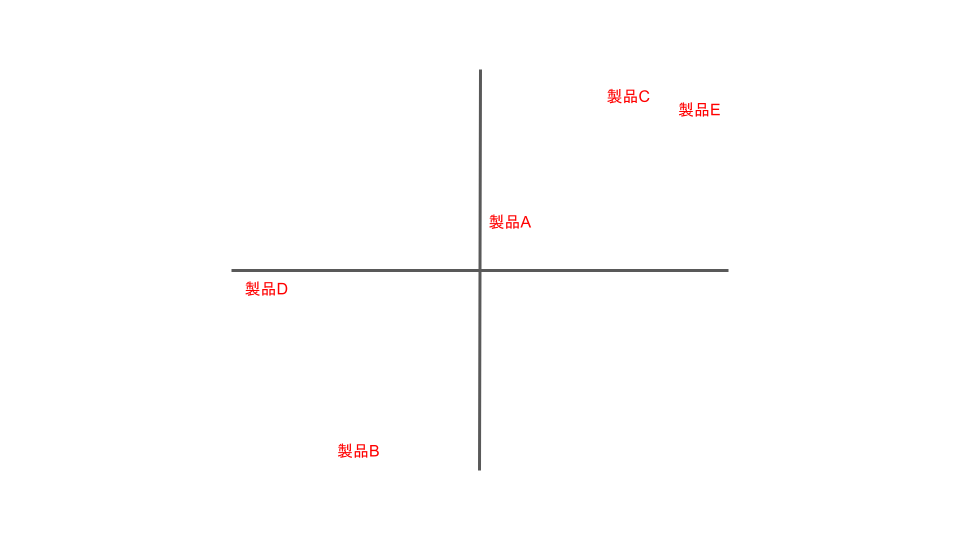
結果は以下のようになりました。

製品Cと製品Eは近い位置にあり、似たポジションの製品だということが分かります。
反対に製品BとDはそれらの製品とは違うポジションを狙った製品だということも分かります。
このマップから、他社の製品と差別化した製品を作るならばグラフの左上や右下に位置できるような製品を製作するのが有効だと考えられます。
しかしそのためには横軸と縦軸が何を意味しているのか、考察する必要があります。
まずは横軸に関して考えてみます。
製品B,Dと製品C,Eで比較してみると、製品B,Dは比較的安価でコストパフォーマンスを売りにしたまくらであるのに対し、製品C,Eは高級感を売りにした製品であるようです。
このことから横軸は値段と強く関連した軸だと考えられます。
次に縦軸に関して考えてみます。
製品C,Eと製品Bで反対の性質があり、製品A,Dは特徴を持たない要素を検証してみると、まくらの反発の強さが該当しました。
製品C,Eは高反発、製品Bは低反発のまくらでした。
これらの考察をもとに、ポジショニングマップを以下のようにアップデートしました。
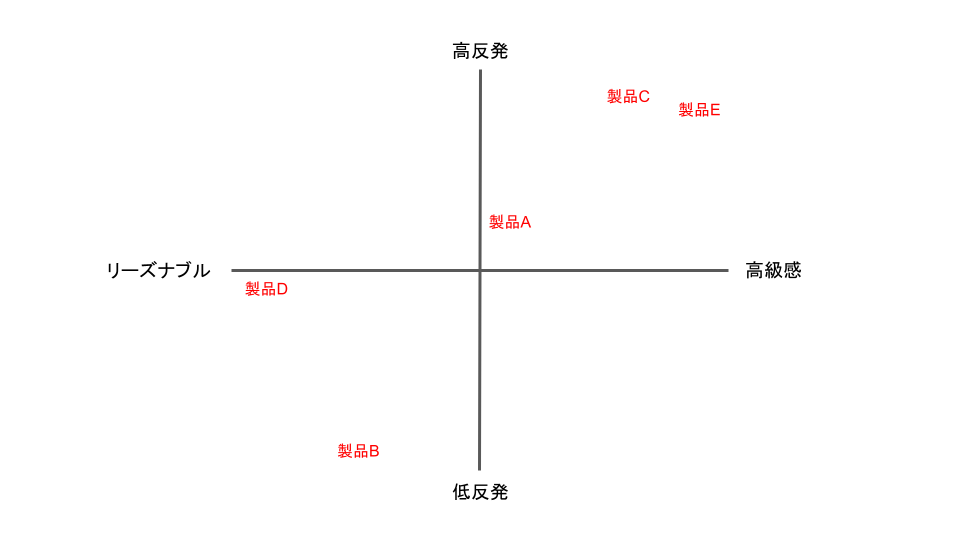
他社のまくらと差別化するためには、「リーズナブルな高反発まくら」か「高級感のある低反発まくら」が良さそうであることが分かりました。
現状ではどちらの製品の方が市場に求められていて、売上に貢献するかまでは分かりません。
消費者の需要や開発費用などを加味して、最終的にどちらのまくらを開発するか詳細に検討していくことになりました。
以上の事例は自社製品の開発方針を決める上で、多次元尺度構成法を活用したケースです。
この例のように多次元尺度構成法は、最初のおおまかな方針を決める上で活用されるケースが大半です。
4.まとめ
最後におさらいをしましょう。
- 多次元尺度構成法とは、対象の類似度を元にポジショニングマップを作成する分析手法
- マーケティング分野において、ポジショニング戦略や顧客属性の特徴を把握、検討する際に活用される
- 多次元尺度構成法を実施する際には、事前に距離行列と呼ばれる分析用データの準備が必要
- 多次元尺度構成法のメリットは、複雑な要素を要約して簡単に分かりやすいグラフを作成できる点
- ポジショニングマップはざっくりとした方針を決める際に役立つが、詳細な検証を行う際には別の分析手法を使う必要があるため注意が必要
- 分析目的を明確にして、主成分分析やクラスター分析と使い分ける必要がある
ポジショニング戦略を検討する上でポジショニングマップは非常に有用なため、多次元尺度構成法が活用できる機会は多くあります。
多次元尺度構成法を活用すれば簡単にポジショニングマップを作成できるため、今まで活用したことがない方は、ぜひ一度活用してみてください。
最後までお読みいただきありがとうございました。


