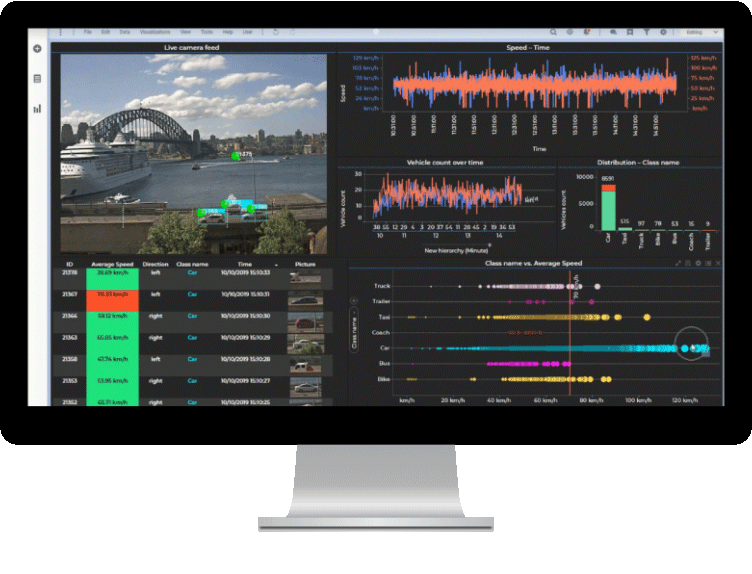
クラスター分析とは?
手順や用途、アルゴリズムの種類について
クラスター分析とは、大量のデータの中から、似ている特徴を持つものをグループ化し、そのグループ(クラスター)を特定するデータ分析手法です。
クラスター分析とは?
クラスター分析とは、データセット内の自然に発生するグループであるクラスターを探索するデータ分析手法です。クラスター分析は、あらかじめ定義されたグループに各データをグループ分けする必要がないため、教師なし学習方法と呼ばれます。教師なし学習では、ラベルやクラスを事前に定義しなくても、データから洞察が得られます。優れたクラスタリングアルゴリズムは、クラスター内では類似性が高く、クラスター間では類似性が低いことを保証します。
データのクラスタリング問題の例
クラスター分析のシンプルな使用例として、小売店舗を売上に基づいてグループ化することが挙げられます。たとえば、あるカフェが市内に8店舗あるとします。以下の表は、1日あたりのカプチーノとアイスコーヒーの販売実績を示しています。
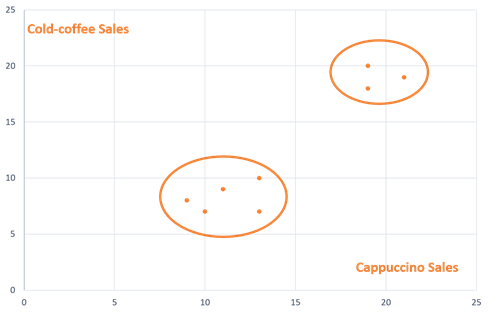
以下のグラフは、各店舗のカプチーノとアイスコーヒーの売上をそれぞれ X 軸と Y 軸にプロットしたものです。この例では、データ数が限られていたため、自然に発生した2つのカフェ店舗のクラスターをグラフ上にプロットし、手作業で可視化することは容易でした。しかし、数千ものデータ数になると、クラスター分析アルゴリズムを使用して、各データを異なるクラスターに分割する必要があります。
クラスター分析の用途
クラスター分析は、主に2つの方法で使用されます。
- データグループ化に関連する問題を解決するための単独のツール
- さまざまな機械学習アルゴリズムの前処理ステップ
単独のツールとしてのクラスター分析
マーケティング
マーケティングでは、クラスター分析を使用して、顧客を購入パターンや興味に基づいて異なる集団に分類することができます。これらは顧客ペルソナとして知られています。組織は、異なる顧客クラスターに対して異なるマーケティング戦略を適用します。
金融におけるリスク分析
金融機関は、銀行残高や負債に基づいて、顧客をさまざまなリスクカテゴリに分類するために、さまざまなクラスター分析アルゴリズムを使用します。ローン、保険、またはクレジットカードの承認時には、これらのクラスター分類が意思決定を支援するために使用されます。
不動産
インフラストラクチャの専門家は、住宅の規模、立地、市場価値に基づいてグループ化するためにクラスタリングを使用します。この情報は、都市の中の異なる地域の不動産ポテンシャルを評価するために使用されます。
機械学習の前処理としてのクラスター分析
クラスター分析は、さまざまな機械学習アルゴリズムの前処理としてよく使用されます。 分類アルゴリズムは、広範なデータセットに対してクラスター分析を実行し、明らかに意味のあるグループに属するデータを除外します。その後、削減された残った各データに対して、高度なデータ分類手法を適用できます。データセットが小さくなると、計算時間が大幅に短縮されます。同じ方法を逆に使用することもでき、クラスター分析アルゴリズムを使用してノイズまたは外れ値データを除外することができます。 教師あり学習アルゴリズムを実行する前に、まず入力データに対してクラスター分析を実行して、データの自然なクラスターを把握することがあります。
主なクラスター分析アルゴリズム
クラスター分析アルゴリズムは、通常、以下のカテゴリに属します。
- パーティションベースのアルゴリズム
- 階層的アルゴリズム
- 密度ベースのアルゴリズム
- グリッドベースのアルゴリズム
- モデルベースのアルゴリズム
- 制約ベースのアルゴリズム
- 外れ値分析アルゴリズム
各アルゴリズムはそれ自体が複雑であり、ある分析には適しているが、他の分析には適していない場合があります。
クラスター分析のためのパーティションアルゴリズム
この方法では、アルゴリズムは複数の初期クラスターから開始します。その後、最適なパーティションが形成されるまで、各データを異なるクラスターに反復して再配置します。K-meansクラスタリングアルゴリズムは、最も人気のあるクラスタリングアルゴリズムの1つです。
以下は、K-meansクラスタリングがどのように機能するかを示した例です。
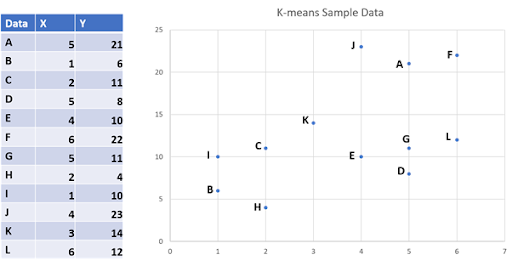
ステップ1:クラスターの決定
アルゴリズムのためのクラスター数「K」を決定します。例えば、K=3とします。アルゴリズムは、上記の12個のデータポイントを3つのクラスターに分割します。Kの数は任意の値でかまいません。それに応じて、クラスタリングの正確さが変わる可能性もありますが、Kの最適な値を決定できるアルゴリズムもあります。
ステップ2:データポイントの選択
K=3の場合、任意の3つのデータポイントを初期平均とします。この例では、点C、D、Eが初期平均として選択されています。K-meansアルゴリズムは、どんな点でも初期平均として取ることができることに注意してください。
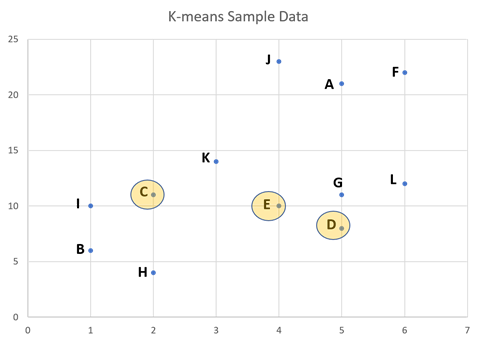
ステップ3:距離の計算
データセット内の各点から各初期クラスター平均までの距離を計算します。3つのクラスター平均C、D、Eがランダムに選択されています。サンプル内の各データポイントについて、これらの3つの平均からの距離を計算します。2点(X1、Y1)と(X2、Y2)間のユークリッド距離は以下のように定義されます。
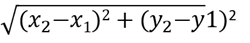
ステップ3の後、表に初期平均C、D、Eからの各データポイントの距離が表示されます。 各データは、最小距離に基づいてクラスターに追加されます。例えば、点Aは初期平均Cから最小距離にあります。これは、Aが平均Cのクラスターに属することを意味します。最初のステップの後、クラスターが得られます。
ステップ4:反復 - 新しい平均の計算
これで初期クラスターが見えやすくなりました。次のステップでは、3つの新しいクラスター平均を計算します。特定のクラスター内のすべてのデータを取り、平均を計算します。
「C」クラスターの新しいクラスター平均 =(5 + 2 + 6 + 1 + 4 + 3 + 6/7、21 + 11 + 22 + 10 + 23 + 14 + 12/7)=(3.85、16.14)、この点をXとします。
「D」クラスターの新しいクラスター平均 =(1 + 2 + 5/3、6 + 8 + 4/3)=(2.66、6)、この点をYとします。
「E」クラスターの新しいクラスター平均 =(4 + 5/2、10 + 11/2)=(4.5、10.5)。この点をZとします。
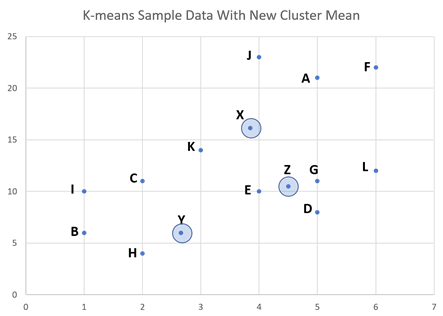
ステップ5:反復 - 新しい平均から各データポイントの距離を計算
新しく計算されたクラスター平均X、Y、およびZからすべてのデータとの距離を調べるために、ステップ3を繰り返します。この新しい反復では、データC、D、I、Lの最小距離が変更されたことがわかります。これらは、下図のようなクラスターに属しています。
そして、いくつかのデータクラスターを変更したので、K-means反復を続ける必要があります。
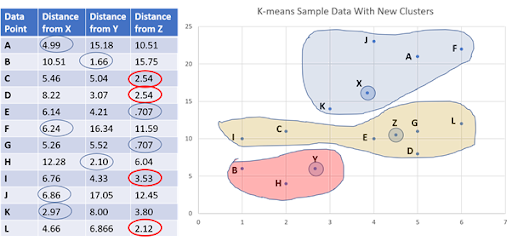
ステップ6:反復 - 新しい平均と新しいクラスターの計算
データポイントC、D、I、Lがクラスターを変更したため、ステップ4と同様に新しいクラスター平均を計算する必要があります。これにより、特定のクラスター内のすべてのデータが取得され、平均が計算されます。次に、ステップ5と同様に、各データから新しいクラスター平均までの距離が計算されます。距離に基づいて、データは最小距離を持つクラスターに割り当てられます。
K-meansアルゴリズムはいつ終了するのか
K-meansは反復的なパーティションアルゴリズムです。
- 始めにクラスター数(K)を決定します。上記の例では、K=3です。
- K個のデータポイントをランダムに初期クラスター平均として割り当てます。
- 全データがクラスターを変更しなくなるまで、以下の手順を繰り返します。
- 各データからクラスター平均までの平均距離を計算します。
- 最小距離を持つクラスターにデータポイントを割り当てます。
- データポイントがクラスターを変更したかどうかを確認します。
新しい反復では、すべてのデータが前のクラスターに残っている場合、K-meansアルゴリズムは終了します。これは、局所的に最適な解が得られたことを意味します。
K-Medoid パーティションベースクラスタリングアルゴリズム
K-medoidsアルゴリズムは、別種のパーティションベースのクラスタリングアルゴリズムです。K-medoidsアルゴリズムは、クラスターの代表点としてmedoidを選択します。K-medoidsアルゴリズムは、特定のクラスター内の他のすべてのデータから最小限の相違度(dissimilarity)を持つデータを見つけようとします。相違度が最小になるまで、K-medoidsアルゴリズムはデータセットを再分割します。K-meansアルゴリズムは、しばしば最小二乗距離(ユークリッド距離)を使用しますが、K-medoidアルゴリズムは、マンハッタン距離のような絶対値距離を使用して2つのデータ間の相違度を測定することがよくあります。
K-medoidアルゴリズムの標準的な実装は、Partition Around Medoids(PAM)アルゴリズムです。以下は、PAMアルゴリズムの基本的な手順です。
- データが分割されるクラスター数Kの値を選択します。
- データのうちK個をランダムにmedoidとして選択します。
- データセット内のすべてのデータ(Xi、Yi)について、上記で選択されたmedoidとの間の相違測定をします。相違度を測定するためによく使用される方法は、マンハッタン距離です。
| Xi – Ci| + | Yi - Cj|(Ci、Cjはmedoidを表します)。
- 各データ(Xi、Yi)は、相違度が最小になるクラスターに割り当てられます。
- 上記の各クラスターについて、各データポイントの相違度の合計である総コストを計算します。
- 新しいmedoidとしてメソッド以外の点をランダムに選択し、手順3-5を繰り返します。
- クラスターに変更がなくなったら停止します。
K-MeansとK-Medoidアルゴリズムの比較
K-meansアルゴリズムはシンプルですが、データにノイズや外れ値が多い場合、良い結果を出しません。K-medoid法は、そのような場合にはより堅牢です。ただし、PAMのようなK-medoidアルゴリズムは、データセットが小さい場合にしか役立ちません。データセットのサイズが増加すると、K-medoidアルゴリズムの計算時間は指数関数的に増加します。
分割アルゴリズム
名前が示すように、分割アルゴリズムは最初にすべてのデータを単一のクラスターに割り当てます。それから、最も似ていないクラスターに分割します。その後、アルゴリズムはこれらのクラスターを再帰的に分割し、最適な解が得られるまで分割を続けます。分割アルゴリズムは、トップダウンクラスタリング方法としても知られています。
Agglomerative アルゴリズム
これらのアルゴリズムは、最初に各データを異なるクラスターに割り当てることから始まります。その後、アルゴリズムは最も似ているクラスターを再帰的に結合し、最適な解が得られるまで続けます。集積アルゴリズムは、ボトムアップクラスタリング方法としても知られています。
Agglomerative クラスタリングアルゴリズムの例
下記は5つのデータ間の距離行列です。データ間の距離はユークリッド距離、マンハッタン距離、あるいは他の距離計算法で計算できます。データXからデータYへの距離と、データYからデータXへの距離は常に同じであるため、距離行列は常に対称行列です。下記はこの距離行列に基づいて、Agglomerative(ボトムアップ)クラスタリングアルゴリズムを適用した例です。
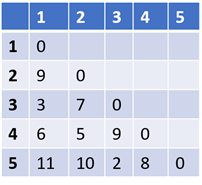
ステップ1:距離行列で、距離が最小の2つの点を見つけます。上記の例では、点3と5です。二つの点の間の距離は2です。それらを単一のクラスターに入れます。
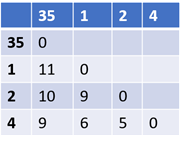
ステップ2:点3と5を削除し、「35」というクラスターに置き換え、新しい距離行列を作成します。作成するためには、すべてのデータとクラスター「35」の間の距離を計算する必要があります。この距離を決定するためには、さまざまな方法があります。 この例では、次の方法を使用して距離を計算しました。 クラスター「35」から点Xまでの距離=最小(距離(X、3)、距離(X、5))。この方法に基づく更新された距離行列は次のとおりです。
ステップ3:すべてのデータが1つのクラスターにグループ化されるまで、ステップ2を繰り返します。現在の例では、6回の反復が必要です。以下の図は、クラスターの形を示しています。この表現はデンドログラムとして知られています。この表現では、Y軸は2つのデータ間の距離を表します。たとえば、点3と5の距離は2です。
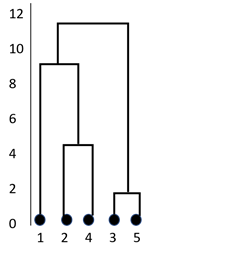
ステップ4:上記のように、すべてのデータがクラスタリングされたら、保持する必要があるクラスターの数を決定します。すべての階層的クラスタリングアルゴリズムは最終的に単一のクラスターを生成するため、それは難しい決定です。階層的クラスタリングアルゴリズムがデータを分割した後、最適なクラスターの数を決定するために使用できる方法がいくつかあります。
密度ベースのクラスタリングアルゴリズム
これらのアルゴリズムは、クラスターが常に周囲のデータ空間よりも密集しているという考え方に基づいています。密度ベースのアルゴリズムは、単一のデータから始まり、その近傍のデータを探索します。最初の点の近傍にある点は、単一のクラスターに含まれます。近傍の定義は、アルゴリズムの実装によって異なります。ノイズを伴う空間クラスタリング(DBSCAN)は、このカテゴリーで人気のあるクラスタリングアルゴリズムです。
グリッドベースのクラスタリングアルゴリズム
グリッドベースのクラスタリングアルゴリズムは、密度ベースのアルゴリズムに似ています。データ空間は、グリッドとして知られるいくつかの小さな単位に分割されます。各データは、特定のグリッドに割り当てられます。その後、アルゴリズムは各グリッドの密度を計算します。密度が閾値よりも低いグリッドは除外されます。次に、アルゴリズムは、密集したグリッドの隣接グループからクラスターを形成します。統計情報グリッド(STING)とクエスト内のクラスタリング(CLIQUE)は、2つのよく使われるグリッドベースのアルゴリズムです。 上記で説明したアルゴリズムに加えて、クラスタリング分析には、モデルベースのクラスタリング、制約ベースのクラスタリング、外れ値分析アルゴリズムが含まれます。
クラスタリング分析アルゴリズムの利点と欠点
| アルゴリズム | 利点 | 欠点 |
|---|---|---|
| パーティションベースのクラスタリングアルゴリズム |
|
|
| 階層的クラスタリングアルゴリズム |
|
|
| 密度ベースのクラスタリングアルゴリズム |
|
|
| グリッドベースのクラスタリングアルゴリズム |
|
|
関連製品
-
Spotfire組織全体でのデータ分析・活用を実現するオールインワンのデータ分析ソフトウェア詳しく見る
高い評価と実績